Weixian Shi

• About me
• Blog

DQN (Deep Q-learning)及其各种升级版本

《强化学习基础》

上一篇：《强化学习基础》- 时序差分(TD)、SARSA、Q-learning

价值函数的近似表示

前面提到，无论是动态规划DP，蒙特卡罗方法MC，还是时序差分TD，使用的状态都是离散的有限个状态集合S。此时问题的规模比较小，比较容易求解。但是当状态集合很大甚至状态是连续时，就无法学习(比如Q-learning的Q表过大)

解决办法：采用近似方法表示状态的价值函数。

• 引入一个状态价值函数 $\hat{v}$, 这个函数由参数 $w$ 描述, 并接受状态 $s$ 作为输入，计算后得到状态 $s$ 的价值，即：$\hat{v}(s, w) \approx v_{\pi}(s)$;

• 同样的，引入动作价值函数 $\hat{q}$：$\hat{q}(s, a, w) \approx q_{\pi}(s, a)$

• 而 $\hat{v}$ 或者 $\hat{q}$ 可以是一个线性函数、决策树、KNN、傅里叶变换甚至是神经网络等等函数

• 如下图，近似过程可以分为三种情况：

  1. 对于状态价值函数，神经网络的输入是状态s的特征向量, 输出是状态价值 $\hat{v}(s, w)$
  2. 对于动作价值函数
     1. 输入状态s的特征向量和动作a，输出对应的动作价值 $\hat{q}(s, a, w)$
     2. 只输入状态s的特征向量，动作集合有多少个动作就有多少个输出 $\hat{q}\left(s, a_{i}, w\right)$

Deep Q-learning (基于 NIPS 2013)

又称DQN，算法思路来源于Q-learning，区别在于它的Q值不是直接通过状态s和动作来计算，而是通过神经网络计算近似计算

重点：

1. DQN的输入是我们的状态s对应的状态向量 $\phi(s)$, 输出是所有动作在该状态下的动作价值函数Q。Q网络可以是DNN，CNN或者RNN，没有具体的网络结构要求。
2. DQN主要使用的技巧是经验回放（experience replay）, 即将每次和环境交互得到的奖励与状态更新情况都保存起来，用于后面目标Q值的更新。作用类似于Q-learning中的Q表
3. 通过经验回放得到的目标Q值和通过Q网络计算的Q值是有误差的，可以通过梯度的反向传播来更新神经网络的参数w，当w收敛后，我们的就得到的近似的Q值计算方法，进而贪婪策略也就求出来了。

算法流程：

Note: 实际应用中，为了算法较好的收敛，探索率$\varepsilon$需要随着迭代的进行而变小。

缺点：Q网络有时候不一定能收敛！(由于循环依赖问题，下面马上解释)

DQN升级版本

Nature DQN

从上面可知，DQN目标Q值的计算公式为： \(y_{j}=\left\{\begin{array}{ll} R_{j} & is\_end_j \space is \space true \\ R_{j}+\gamma \max _{a^{\prime}} Q\left(\phi\left(S_{j}^{\prime}\right), A_{j}^{\prime}, w\right) & else \end{array}\right.\)

• 这里目标Q值的计算使用到了当前要训练的Q网络参数来计算 $Q\left(\phi\left(S_{j}^{\prime}\right), A_{j}^{\prime}, w\right)$;
• 而实际上, 我们又希望通过 $y_{j}$ 来后续更新Q网络参数(减小损失函数值，上述算法步骤7)。
• 这样两者循环依赖, 迭代起来两者的相关性就太强了。不利于算法的收敛。

Nature DQN 思想：用两个Q网络来减少目标Q值计算和要更新Q网络参数之间的依赖关系。一个当前Q网络 $Q$ 用来选择动作，更新模型参数; 另一个目标Q网络 $Q^{\prime}$ 用于计算目标Q值。目标Q网络 $Q^{\prime}$ 的网络参数不需要迭代更新，而是每隔一段时间从当前Q网络 $Q$ 复制过来，即延时更新，这样可以减少目标Q值和当前的Q值相关性。公式变为： \(y_{j}=\left\{\begin{array}{ll} R_{j} & is\_end_j \space is \space true \\ R_{j}+\gamma \max _{a^{\prime}} Q^{\prime}\left(\phi\left(S_{j}^{\prime}\right), A_{j}^{\prime}, w\right) & else \end{array}\right.\)

Note: 两个网络的结构需要一致，才能复制网络参数。

与DQN相比，除了这一点不同，其余均一致！

算法流程：

Note: 计算 $y_j$ 时用的是目标网络 $Q^{\prime}$，而神经网络反向传播时用的是当前网络 $Q$。并每隔 $C$ 次迭代，将当前网络 $Q$ 的网络参数复制到目标网络 $Q^{\prime}$。

Double DQN (DDQN)

无论是Q-learning, DQN, 还是Nature DQN，均采用贪婪法来计算目标样本的Q值。如： \(y_{j}=\left\{\begin{array}{ll} R_{j} & i s_{-} e n d_{j} \text { is true } \\ R_{j}+\gamma \max _{a^{\prime}} Q^{\prime}\left(\phi\left(S_{j}^{\prime}\right), A_{j}^{\prime}, w^{\prime}\right) & i s_{-} e n d_{j} \text { is false } \end{array}\right.\) 使用贪婪法(即max)虽然可以快速让Q值向可能的优化目标靠拢，但是很容易过犹不及，导致过度估计(Over Estimation)，即最终得到的算法模型有很大的偏差(bias)

DDQN思想：与Nature DQN一样，拥有两个结构一样的Q网络，然后在其基础上，通过解耦目标Q值动作的选择和目标Q值的计算这两步，来消除过度估计的问题。对比如下：

• Nature DQN中，对于非终止状态的Q值计算：$y_{j}=R_{j}+\gamma \max {a^{\prime}} Q^{\prime}\left(\phi\left(S{j}^{\prime}\right), A_{j}^{\prime}, w^{\prime}\right)$

• 而在DDQN中，对于非终止状态的Q值的计算公式为：$y_{j}=R_{j}+\gamma Q^{\prime}\left(\phi\left(S_{j}^{\prime}\right), \arg \max {a^{\prime}} Q\left(\phi\left(S{j}^{\prime}\right), a, w\right), w^{\prime}\right)$

  • 首先不再是直接在目标Q网络里面找各个动作中最大Q值，而是先在当前Q网络中先找出最大Q值对应的动作，即：$a^{\max }\left(S_{j}^{\prime}, w\right)=\arg \max {a^{\prime}} Q\left(\phi\left(S{j}^{\prime}\right), a, w\right)$

  • 然后利用这个选择出来的动作 $a^{\max }\left(S_{j}^{\prime}, w\right)$ 在目标网络里面去计算目标Q值。即： \(y_{j}=R_{j}+\gamma Q^{\prime}\left(\phi\left(S_{j}^{\prime}\right), a^{\max }\left(S_{j}^{\prime}, w\right), w^{\prime}\right)\)

Note: 除了这一点与Nature DQN 不同外，其他均一致。

Prioritized Replay DQN

之前的DQN，如: Nature DQN, DDQN 等在做经验回放时，样本的采样都是同等概率。仅仅只保存和环境交互得到的样本状态，动作，奖励等数据，没有优先级。

但是在经验回放池里面的不同的样本由于TD误差的不同，对我们反向传播的作用是不一样的。

• 在Q网络中，TD误差就是目标Q网络计算的目标Q值和当前Q网络计算的Q值之间的差距。
• TD误差越大，那么对我们反向传播的作用越大。
• 而TD误差小的样本，由于TD误差小，对反向梯度的计算影响不大。

Prioritized Replay DQN 思想：如果TD误差的绝对值

δ(t)

较大的样本更容易被采样，则我们的算法会比较容易收敛。于是可以基于DDQN, 根据每个样本的TD误差绝对值 $

\delta(t)

$，给定该样本的优先级正比于 $

\delta(t)

$，将这个优先级的值存入经验回放池。

经验池设计：由于引入优先级，为了保证高优先级的样本能够更容易被采样，同时低优先级的样本也要有可能被采样，不能直接采用贪婪法来采样，这里我们引入SumTree。

SumTree

一种二叉树类型的数据结构，所有叶子节点存储优先级 $p_i$ ，所有父节点为子节点之和，所以这棵树的根节点即为所有叶子节点的和。除此之外，所有的样本数据均保存在叶子节点，内部节点没有样本数据。

sum-tree 的前世今生

英文原文。

在没有优先级时，我们可以直接使用random函数采样。

当有优先级时，首先我们划分出几个不同的优先级，比如8个，如下图。

1. 最简单的采样方法：

   • 比如说总概率为68，分为8个区域，每个区域都具有一定的概率数(代表优先级高低)，图中[0,17]的优先级为17(不应该是18，后面的也是，都应该减1，加起来才是68图上有误)，[18-30]的优先级为12等等。

   • 采样时首先在[0,67]中随机抽取一个数，然后查询该数落在哪个区域，然后再在该区域随机采样一个样本。这样我们发现对于优先级高的区域，被采样到的概率也会更高。
   • 同时，我们可以知道，这样的方式并不需要对优先级进行事先排序，如下图，这样也是一样的。
2. sum-tree

   • 上述方式虽然可行，但是它的查询时间复杂度为$O(n)$, 如果区域很多的话，会耗费不少时间。于是推出了复杂度为$0(logn)$的Sum Tree.

   • 如下图，所有的样本数据均保存在叶子节点，同时叶子节点还保存了他们的优先级大小，而内部节点只保存子节点的优先级和。例如，当我们在0-67中随机数采样到了24，此时24小于26，于是往左子树查找，24大于22，于是24落在26的右子树，而26-24=2,2大于1小于3，而是最终落在了从左往右第4个叶节点；然后我们再在该叶节点采样出一个数据样本即可！

     

以上讲到的优先级问题是与DDQN第一个不同点。

第二个不同点：

• 之前的损失函数为 $\frac{1}{m} \sum_{j=1}^{m}\left(y_{j}-Q\left(\phi\left(S_{j}\right), A_{j}, w\right)\right)^{2}$。

• 而现在改为 $\frac{1}{m} \sum_{j=1}^{m} w_{j}\left(y_{j}-Q\left(\phi\left(S_{j}\right), A_{j}, w\right)\right)^{2}$。其中 $w_{j}$ 是第j个样本的优先级权重, 由TD误差 $

  \delta(t)

  $ 归一化得到。

第三个不同点：当我们对Q网络参数进行了梯度更新后，需要重新计算TD误差，并将TD误差更新到SunTree上面。

其余均与DDQN一致。

算法流程：原地址

Dueling DQN

DDQN中，通过优化目标Q值的计算来优化算法，在Prioritized Replay DQN中，通过优化经验回放池按权重采样来进一步优化算法。而在Dueling DQN中，我们尝试通过优化神经网络的结构来优化算法。

如何优化网络结构呢?

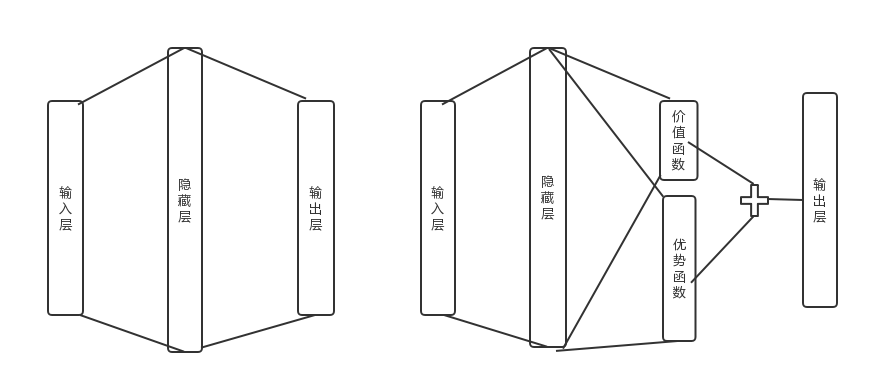
Dueling DQN考虑将Q网络分成两部分，第一部分是仅仅与状态 $S$ 有关, 与具体要采用的动作 $A$ 无关, 这部分我们叫做价值函数部分, 记做 $V(S, w, \alpha)$,第二部分同时与状态状态 $S$ 和动作 $A$ 有关, 这部分叫做优劫函数(Advantage Function)部分,记为 $A(S, A, w, \beta)$,那么最終我们的 价值函数可以重新表示为: \(Q(S, A, w, \alpha, \beta)=V(S, w, \alpha)+A(S, A, w, \beta)\)

如下图所示，左边为DDQN等其他DQN网络结构，右边为Dueling DQN, 可以看到，最终Q网络的输出由价格函数网络的输出和优势函数网络的输出线性组合得到。其他流程均一致